Calculate Weld Metal Volume

(and other formula)

Self Study Program,

"Welding Math and Science;" 87 Pages, Part # WMS

This program provides basic information to help welding students and welding supervisors understand welding process characteristics using math and science.  Includes and Appendix with subjects like Reading a Ruler and Basic Math Functions. 

CLICK to See Program Details       CLICK for Purchase Page  

You Can Start From Basics and Calculate any Weld Volume.

First some formula to calculate Area:

The basic formula for the Area of Rectangle is:

L (length) _* W (width) = Area  (Note: We'll use  _*  to indicate multiply since that is what is used on a Spreadsheet.)

Here is a neat way to check your answer called Dimensional Analysis.  Big word but it means checking the dimensions to be sure the result is what you are looking for and helps to be sure your formula is correct:

In this case: L inches _* W inches = Area inch² (Since in _* in = in ²  )

Dimensional Analysis verifies you correctly multiplied in _* in and got in²

Note: a Square is a special case of a rectangle where both sides are the same so the area can be stated as one side times itself or Area = S² (Length of a side squared)

Let's now define the Volume of a Rectangular Block.

W in _* L in _* D (Depth) in = Volume in ³

We multiplied three dimensions in inches so got in ³ or cubic inches as an answer. 

The following are some formula for calculating the area of additional shapes we’ll use to define weld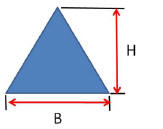 volume in a joint:

For the Triangle on the right:  Area = B _* H / 2 

Note it is like calculating the Area of  a Rectangle and dividing by 2.

This formula works for any size and shape Triangle.  Look at the Triangle below left.  Below  right are picture examples that help show why this equation works for any shape Triangle:

By duplicating the Blue Triangle and rearranging pieces  we can construct a rectangle:

Referring to the three pictures on the right:

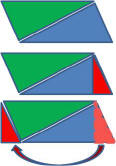
1) In the top picture the Blue Triangle is copied and turned upside down  It is shown in Green.

2) In the middle picture we make a small Red Triangle to create a straight perpendicular side on the Blue Triangle.

3) In the bottom picture the Red Triangle is moved to the left side making a straight side on the Green Triangle.

4) That makes a Rectangle with one side still equal to B and the other H. 

5) The AREA as defined for a Rectangle is B _* H.  But remember we duplicated the Blue Triangle so to get the AREA of the Original Blue Triangle we have to divide by 2 hence the formula: Area = B _* H / 2

Area of a Segment (Weld Reinforcement)

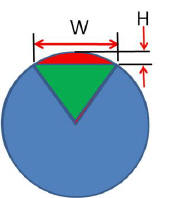This is one Area that is often used in calculating weld metal area and volume; it is called the area of a Circle Segment and shown in Red on the photo left.  This is what is used to calculate the area of Weld Reinforcement.  The accurate way to do this is to calculate the area of a segment of Radius R (that is the combined Green and Red Areas;) use the length of the Cord W (width of weld) and subtract the area of the triangle formed by the Cord and distance from the Center of the Circle and the Cord (the Green Area.)  This leaves the Area between the Cord  and the Outer Area of the Circle (Red Area) or Weld Reinforcement in our case.

However we would have to estimate the Radius of the circle making the reinforcement and the angle of that Segment.  Not an easy item to estimate.  Since we know the weld bead height (or the desired maximum height by code, usually 3/32 or 1/8 inch) and the weld height is much smaller than the weld width we can use a method that estimates the area and  is probably better than estimating the radius.  The formula is:

Approximate Area of a Segment (Weld Reinforcement) = (2 H _* W) / 3 + H ² / 2W

Since weld reinforcement is not a perfect circle, the value obtained is sufficiently accurate for any engineering calculations needed.  In fact since weld reinforcement is not a portion of a perfect circle this approach may be closer to the actual area/volume!  Having checked several typical weld reinforcements dimensions you can use 72% of the Area of a Rectangle  for the estimate of reinforcement.

With these basic shapes you can calculate the area of almost all welds. 

Look at the following examples of the of weld joints; the weld area can be arranged into Triangles, Rectangles and Segments.

To calculate the weld metal volume that must be added to a weld joint you simply multiply the Area times the Length in the same dimensions.  Therefore if the length is given in feet convert it to inches so all dimensions are in inches.  Therefore Area in² * Length in = Volume in³.  Remember dimensional analysis works to check your work in ² * in = in³.

Calculate Pounds of Welding Materials Needed:

Now  the Volume of weld metal you’ll need to add is known , how much wire will you need?  The following are some material densities:

Steel weights: 0.284 lb / in³; Aluminum = 0.098 lb / in³ depending somewhat on alloy and Stainless Steel 0.29 lb / in³ again depending on the alloy.

So to get lbs of weld metal needed do you just multiply the volume by the density of the material?

Is that how much you should purchase?

No!

You Must Account for Losses.

For example when Stick Welding the electrode purchased includes flux, you’ll  also throw away the stub and some of what your depositing will become wasted spatter.  The factor that estimates the amount of welding electrode purchased that deposits as weld metal is called Deposition Efficiency.  Stick Electrodes, as you’d expect, have the lowest values.  Depending on the length, type of electrode and the amount of stub being thrown away the Deposition Efficiency can vary from as low as 40%, meaning only 40% of what you purchase will become weld metal to a high of 60%.  For general calculations you can use 50%.

The following are some values you can use for various welding processes:

Submerged Arc Welding = 99% for wire

MIG Welding with Solid Wire = 97% with Argon Based Shielding and 96% with CO₂

MIG Welding with Metal Cored Wire = 94%

Gas Shielded Flux Cored Wire Welding = 90 to 93%

Self Shielded (Gasless) Flux Cored Wire Welding = 78 to 80%

Stick Electrode Welding = ~50% +/- 10%

Therefore divide the weld metal needed by the Deposition Efficiency (as a decimal, i.e. 93% = 0.93) to get how much of the particular filler material being used needs to be purchased. Therefore if you find 55 lbs of weld metal is needed then you'll need to purchase 55 lbs/0.93 = 59 lbs of wire or 55 lbs/0.50 = 110 lbs of Stick electrode.

One Other Calculation often used is the length of wire to make a pound.  This defines the needed wire feed speed etc.

We’ll calculate 0.045 solid wire and then give some values you can use:

The area of an 0.045 in diameter wire is = (0.045 ²  * 3.1416) / 4 = 0.00159 in²  

[Note: 3.1416 is the number obtained when dividing the circumference of any circle by its diameter.  It is called by the Greek Letter that Archimedes used in the 3rd Century BC when he utilized the value in his calculations, (π) Pi ]

The Volume per foot = Area _* 12 in / ft = Volume in³ / ft wire = 0.0191 in³ / ft

Weight = Volume / ft _* 0.294 lb / ft = 0.00542 lb / ft.  To get ft / lb divide 1 / (lbs/ft) = 184 ft/lb.

Note how dimensional analysis shows the correct units.  Crunch the numbers and you’ll get:

For metal and flux cored wire the density is somewhat lower than solid wire and is dependent on the specific wire, percentage of outer sheath, amount of iron power versus flux in the core etc.  You could multiply the above values by 1.05 to get an estimate.

Welding Math and Physics PDF

Welder Rap on Gas Video

Purchase

Gas Saving

Products  

Purchase Training

Products

Purchase Wire Feeding Aids